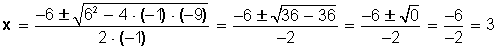Las ecuaciones lineales o de primer grado son del tipo ax + b = 0
con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
PROPIEDADES DE LA ECUACIONES LINEALES
Resolver una ecuación
es calcular el o los valores de la o las incógnitas para que la
igualdad sea verdadera.. Para esto se deben tener presente las siguientes
propiedades de
la igualdad.
Propiedad 1
: Cuando se suma o resta un número
a ambos lados de la igualdad, la igualdad se mantiene.
Propiedad 2
: Cuando se multiplica o divide
por un mismo número, distinto de cero, en ambos lados de la igualdad,
la igualdad se mantiene.
la igualdad se mantiene.
Propiedad 3
: Cuando se eleva a una potencia
distinta de cero ambos miembros de la igualdad, la igualdad se mantiene.
Propiedad 4
: Cuando se extrae la misma
raíz, en ambos lados de la igualdad, la igualdad se mantiene.
Estas Propiedades
de Igualdad son las que se aplican en la resolución de las ecuaciones,
independientemente del tipo de coeficientes numéricos que tenga,
en otras palabras,
siempre se resuelven
las ecuaciones usando los mismos métodos
, lo único diferente
es la forma en que se realizan las operaciones matemáticas con los
números que pertenecen a distintos conjuntos.
Resolución de ecuaciones lineales
En general para resolver una ecuación lineal o de primer grado debemos seguir los siguientes pasos:
1º Quitar paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x en un miembro y los términos independientes en el otro.
4º Reducir los términos semejantes.
5º Despejar la incógnita