Ecuaciones de segundo grado y una incógnita
Sabemos que una ecuación es una relación matemática entre números y letras. Normalmente se trabaja con ecuaciones en las que sólo hay una letra, llamada
incógnita
, que suele ser la
x
.
Resolver la ecuación consiste en encontrar un valor (o varios) que, al sustituirlo por la incógnita, haga que sea cierta la igualdad.
Ese valor es la
solución
de la ecuación.
Ejemplo: Resolver la ecuación
x − 1 = 0
El número que hace que esa ecuación sea cierta es el 1, ya que
1 – 1 = 0
, por lo tanto, 1 es la solución de la ecuación.
Si en la ecuación la incógnita está elevada al cuadrado, decimos que es una
ecuación de segundo grado (llamadas también ecuaciones cuadráticas)
, que se caracterizan porque pueden tener
dos soluciones
(aunque también una sola, e incluso ninguna).
Cualquier ecuación de segundo grado o cuadrática se puede expresar de la siguiente forma:
ax
2
+ bx + c = 0
Donde
a
,
b
y
c
son unos parámetros que habrá que sustituir por los números reales que corresponda en cada caso particular.
Solución de ecuaciones cuadráticas
Hemos visto que una ecuación cuadrática es una ecuación en su forma
ax
2
+ bx + c = 0
, donde
a, b
, y
c
son números reales.
Pero este tipo de ecuación puede presentarse de diferentes formas:
Ejemplos:
9x
2
+ 6x + 10 = 0
a
= 9,
b
= 6,
c
= 10
3x
2
– 9x
+ 0
= 0
a
= 3,
b
= –9,
c = 0
(el cero,
la c
, no se escribe, no está)
–6x
2
+ 0x
+ 10 = 0
a
= -6,
b = 0
, c = 10 (el cero equis,
la b
, no se escribe)
Para resolver la ecuación cuadrática de la forma
ax
2
+ bx + c = 0
(o cualquiera de las formas mostradas), puede usarse cualquiera de los siguientes métodos:
- UTILIZANDO LA FORMULA GENERAL
- FACTORIZACION
EJEMPLO UTILIZANDO LA FORMULA GENERAL
Resolver:
6x − x
2
= 9
Hacemos los cambios necesarios para que la ecuación tenga la forma conocida. Trasponiendo y cambiando de lugar resulta:
− x
2
+ 6x − 9 = 0.
Ahora se identifican las letras:
a = −1 ; b = 6 ; c = −9
; y se aplica la fórmula:
El discriminante (Δ) es igual a cero, por lo cual se producen dos raíces iguales a 3, es decir,
x
1
= x
2
= 3.
POR FACTORIZACION
6X-X2=9
6X-X2-9=9-9
6X-X2-9=0
-X2+6X-9=0
SE MULTIPLICA POR -1 AMBOS LADO DE LA ECUACION PARA QUE a
SEA POSITIVA (ESTO SUCEDE CUANDO ES NEGATIVA a)
X2-6x+9=0
(x-3) (x-3)=0
Se aplica el teorema del factor nulo
(x-3)=0
(x-3)=0
X1=3
X2=3
ECUACIONES DE SEGUNDO GRADO COMPLETA RESUELTA POR LA FORMULA GENERAL.
VER LOS VIDEOS Y COMENTARLOS
ECUACIONES DE SEGUNDO GRADO POR FACTORIZACION CUANDO A =1
FACTORIZACION DE LA FORMA ASPA CUANDO A ES DIFERENTE DE 1
BIBLIOGRAFIAS
https://www.profesorenlinea.cl/matematica/Ecuaciones_Seg_grado.html
https://www.youtube.com/watch?v=IGhjsc8lEKY&pbjreload=10
https://www.youtube.com/watch?v=RChv5xhNTgY&t=272s&pbjreload=10

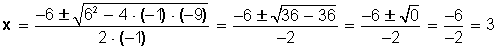
No hay comentarios:
Publicar un comentario